Junction is used to make a "junction point" on a drive. A junction point is sort of like a Shortcut to a folder, except it is handled at a much lower level. To Windows, it's as if the folder it points to is actually at the location it sits in. With it you can make Windows think a program is installed in C: when it is actually held on D: (or any other drive).
Moving software to HDD
Let's say you have Photoshop installed on your SSD, but it takes up a ton of space that you want to reclaim (because the SSD is full and Windows is starting to choke on not having any free MB). Photoshop will typically be installed in c:\program files\adobe. To free up the space you could uninstall photoshop entirely, then run the installer again and put it on D:, but that's a lot of time wasted (and potentially a lot of bandwidth if it has to re-download a bunch of stuff). Instead you can move the adobe folder to D: and use a junction point to make Windows think it's still happily running from C:. To do this you need to:
- Make sure the application in question is not running. Close all open windows, and make sure it hasn't left any icon in the system tray.
- Move the folder from its location on C: (your SSD) to a location on D: (your HDD). Make a D:\program files folder and then using the right mouse button drag the adobe folder over. By using the right mouse button, when you release it a menu will pop up allowing you to select Move.
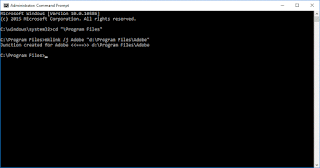
- Now you need to make the junction point. Open the Start menu and type cmd but don't push enter. When it displays the cmd icon, right-click it and Run As Administrator. In the cmd window type:
- Close the cmd window. You should now be able to run Photoshop as normal.
Windows 7
cd "\program files" junction adobe "d:\program files\adobe"
Windows 10 (Junction command was removed from Windows 10; use mklink instead)
cd "\program files" mklink /j adobe "d:\program files\adobe"

Installing to HDD
For a program that only lets you install on C: you either need to make enough room by moving other folders first, or set up the junction before running the installer. For example, Oculus installs in c:\program files\oculus so before installing you can make an oculus folder on D: and then make a junction to it as above; when you run the installer it should see that the oculus folder already exists and install into it.
- Make sure there is no folder at c:\program files\oculus. If you have tried to install and failed it may have left one.
- Make folder d:\program files\oculus
- In a cmd window:
Windows 7
cd "\program files" junction oculus "d:\program files\oculus"
Windows 10
cd "\program files" mklink /j oculus "d:\program files\oculus"
Making Space
If you want to go on a space-saving spree a good program to use is treesize. This will scan your SSD and display all the folders on it sorted by how much space they are taking up, allowing you to quickly see which ones are worth moving over to the HDD. You can use this technique on most programs you find in c:\program files and c:\program files (x86), though you should avoid any Windows folders as they can be a bit temperamental.
No comments:
Post a Comment