In it the presenter shows some code written in classic, old-school imperative C#, and then progressively factors it into his ideal of modern C#.
The algorithm he is implementing takes a sequence of strings, looks at all the ones which can be parsed as an int, and returns the total of the two largest values. It returns -1 as an error code (so we can assume that the numbers passed in are all >= 0).
So, he starts with this:
int GetMagicSum0(IEnumerable<string> items) {
List<int> all = new List<int>();
using (IEnumerator<string> enumerator = items.GetEnumerator()) {
while (enumerator.MoveNext()) {
int number;
if (int.TryParse(enumerator.Current, out number))
all.Add(number);
}
}
if (all.Count < 2)
return -1;
int[] greatestTwo = {all[0], all[1]};
if (greatestTwo[1] > greatestTwo[0]) {
greatestTwo[0] = all[1];
greatestTwo[1] = all[0];
}
for (int i = 2; i < all.Count; i++) {
if (all[i] > greatestTwo[0]) {
greatestTwo[1] = greatestTwo[0];
greatestTwo[0] = all[i];
}
else if (all[i] > greatestTwo[1]) {
greatestTwo[1] = all[i];
}
}
return greatestTwo[0] + greatestTwo[1];
}
And over a few iterations ends up with this:
int GetMagicSum3(IEnumerable<string> items) =>
items.Aggregate((max: 0, next: 0, count: 0), AdvanceRaw, ProduceSum);
int ProduceSum((int max, int next, int count) tuple) =>
tuple.count == 2 ? tuple.max + tuple.next : -1;
(int max, int next, int count) AdvanceRaw((int max, int next, int count) tuple, string item) =>
int.TryParse(item, out int number) ? Advance(tuple, number) : tuple;
(int max, int next, int count) Advance((int max, int next, int count) tuple, int number) => tuple switch
{
(_, _, 0) => (number, 0, 1),
(var max, _, 1) when number > max => (number, max, 2),
(var max, _, 1) => (max, number, 2),
(var max, _, 2) when number > max => (number, max, 2),
(var max, var next, 2) when number > next => (max, number, 2),
_ => tuple,
};
...my blog page is set up pretty narrow, so here's an image of the code that you can zoom (I have nothing against long lines, I wanted to present it as text above so it was copy-pastable):
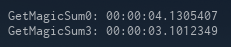
Now, we can argue about which code is better or more readable, but my first thought was that the performance is going to suffer. I was then galvanized by this comment on the video:
Which bear out his response: the functional GetMagicSum3 does indeed run faster than the imperative GetMagicSum0... but you knew there was a "but" coming, right? Did you notice the problem with GetMagicSum0? Go back and look at it and see if you can spot it.
This is the setup for the test program btw:
string CSharpPerformanceTest(int wordCount = 100000000) {
if (wordCount < 2) return "wordCount must be >= 2";
System.Random rng = new((int)System.DateTime.Now.Ticks);
int randomInt() => rng.Next() / 2; // halved so don't overflow
List<string> numbers = new ();
for (int i = 0; i < wordCount; i++)
numbers.Add(randomInt().ToString());
// Then time a call to each GetMagicSumX(numbers);
Did you see what was wrong with GetMagicSum0? The problem with is is it generates a List<string> of the IEnumerable, completely unnecessarily! Horvat does explicitly say that the algorithm isn't the point of the video - the style differences are - but I don't think pointing out that it's making a completely unneeded copy of the data really counts as algorithmic nit-picking!
If we're comparing imperative vs functional then I think it's fair that we use the best possible form of each. We can assume the functional GetMagicSum3 is as good as can be, as the point of the video is to advocate for it, so let's make a good version of GetMagicSum0, we'll call it GetMagicSumA.
Mostly we're simply going to remove the List generated at the start. However, because of how IEnumerable works, setting up the greatestTwo array and then iterating from index 2 would be a pain: you'd need to make an IEnumerator, check Current was there and parsed, MoveNext(), check Current again, until you got two numbers... sounds kind of loop-y. Happily we already have a loop that does all that logic, so we'll simply use it to do all the work. We set up greatestTwo so that it will always be filled out by the first two numbers, by setting it to { -1, -1 }. (If we wanted to handle negative numbers we'd use int.MinValue instead, but as we're only dealing with positive numbers, -1 is more readable). This gets us:
int _GetMagicSumA(IEnumerable<string> items) {
int[] greatestTwo = { -1, -1 };
foreach (string item in items) {
if (int.TryParse(item, out int number)) {
if (number > greatestTwo[0]) {
greatestTwo[1] = greatestTwo[0];
greatestTwo[0] = number;
}
else if (number > greatestTwo[1]) {
greatestTwo[1] = number;
}
}
}
if (greatestTwo[1] == -1) // didn't find two numbers
return -1;
return greatestTwo[0] + greatestTwo[1];
}
Now, clearly I'm partisan; Horvat is bringing his best functional code to the fight, so in balance I'm going to represent imperative as best as I can. To me, that greatestTwo array isn't the clearest thing to reason about in the inner if block, and I'd prefer not to nest quite so deep, so I'm going to refine this to the following semantically identical function:
int GetMagicSumA(IEnumerable<string> items) {
int ultimate = -1;
int penultimate = -1;
foreach (string item in items) {
if (!int.TryParse(item, out int number))
continue;
if (number > ultimate) {
penultimate = ultimate;
ultimate = number;
}
else if (number > penultimate) {
penultimate = number;
}
}
if (penultimate == -1) // didn't find two numbers
return -1;
return ultimate + penultimate;
}
Comparing the readability of the imperative vs functional code is subjective, you can decide which version you find easier to reason about for yourself: below is GetMagicSum3 again for comparison. It takes up 18 lines on the screen, while the above GetMagicSumA takes up 22 (I do tend to space my code out a fair bit).
However, the point of this post is not to argue about style, but about performance, and here are the results:
With the unnecessary List generation removed, the imperative code is indeed faster: GetMagicSum3 takes 1.26x as long as GetMagicSumA.
Follow-up for game developers
This section is for people who really care about performance, so if that's not you please don't get your knickers in a twist.
You probably noticed that in addition to GetMagicSumA, there are two successively faster versions of the function profiled above. If you're using C# for writing games then this bit is for you: DO NOT USE IENUMERABLE. I have never constructed an IEnumerable in any game, ever. For sequences of homogenous data you need two types: List<T> and Array<T>. If your data is sitting in memory there is no reason to use an IEnumerable. If it's being generated an item at a time, then you need to be dealing with that asynchronicity with code that reflects it.
There is a very handy interface called IList, which will accept both List and Array, so is the perfect replacement here. In essence this is the only change between GetMagicSumB and GetMagicSumA:
int GetMagicSumB(IList<string> items) {
int ultimate = -1;
int penultimate = -1;
for (int i = 0; i < items.Count; i++) {
if (!int.TryParse(items[i], out int number))
continue;
if (number > ultimate) {
penultimate = ultimate;
ultimate = number;
}
else if (number > penultimate) {
penultimate = number;
}
}
if (penultimate == -1) // didn't find two numbers
return -1;
return ultimate + penultimate;
}
As you can see the two difference in the code are the parameter type, and using a for instead of a foreach; the result is substantially faster code. Using GetMagicSumB as the baseline, GetMagicSumA takes 1.19x as long as it, and GetMagicSum3 takes 1.5x as long.
Bonus Round
The table of timings contains a final form of the function, GetMagicSumC, which is marginally faster again. It's clear in the original video that the point is not about optimising the algorithm, so this isn't relevant to the post in general. Therefor, an exercise for the reader: how do you modify GetMagicSumB to get GetMagicSumC, and that small gain in performance? Clue:
.